10月号のクローバー通信のコラムで円周率について書きましたが，

あまり詳しいことについて触れることができなかったので，

今日は，そこでは書ききれなかったことを紹介しようと思います。

改めて簡単に説明しておくと（小5で習います），

円周の長さを円の直径で割るといつも同じ値になり，

その値のことを円周率といいます。

さらに，この円周率は“きれいな”分数の形で表すことができない数です。

（こういった数を無理数といい，中3で習います）

そこで，人類はおよそ4000年前からその近似値を求めてきました。

そのような中，およそ2300年前に登場したのが，アルキメデスであり，

アルキメデスは革新的な方法を考え出しました。

それが，次の図のような円に内接する正六角形と，

円に外接する正六角形を利用する方法です。

（内接とは内側からピッタリと接していることであり，

外接とは外側からピッタリと接していることだと考えてください。）

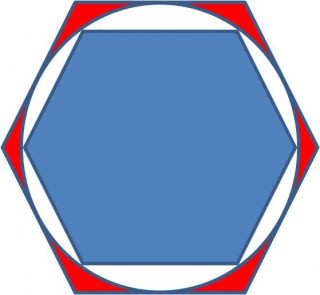
このとき，円周は，

内側の青い正六角形の周りの長さよりも長くなり，

外側の赤い正六角形の周りの長さよりも短くなります。

したがって，青い正六角形の周りの長さと赤い正六角形の周りの長さが分かれば，

円周がだいたい分かるという考えです。

実際には，さらに工夫があるのですが，

アルキメデスは最終的に正96角形を用いて，

（テストで図形の名前を書くときは漢数字を使って下さい）

「円周率は3.14084より大きく，3.14286より小さい」と，

小数点以下2桁まで正しく求めました。

その後，およそ2000年近く，アルキメデスの方法による円周率を求める試みが続き，

1600年ごろにはドイツの数学者ルドルフ・ファン・コイレンが，

正4611686018427387904角形を用いて，小数点以下35桁までを正しく計算しました。

この偉業により，ドイツでは円周率のことをルドルフ数とよぶことがあるそうです。

そして，17世紀になると，微積分学の発展により，

円周率を求める公式が発見され，円周率の計算は飛躍的に進歩しました。

普通に勉強していると，円周率のことも他の多くのことと同じく，

使い方や意味を覚えるだけになってしまうと思いますが，

このような歴史的なことにも，興味を持っていってほしいと思います。

というのもこういった少し本筋を離れた勉強が役に立つことが，

実際のテストであったからです。

次回はそのことについて，書こうと思います。

2011-10-03　高橋